目次
ニュートン算の解き方をマスターしよう
こんにちは!
今日は中学受験でよく登場するニュートン算を解説します。
問題文の中に未知の値がいくつも出てきて、図の書き方、式の作り方がわからない! と、なりがちなニュートン算ですが、一度解き方を覚えてしまえば、どの問題も手順はほぼ一緒です。
問題文が長いせいで敬遠されがちですが、ここで図の書き方と使い方をしっかり身につけていきましょう!
2つの変化する数字に注目!
それでは問題を見ていきましょう。
【例題1】
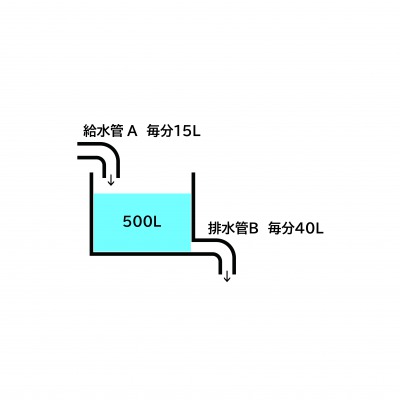
「500Lの水が入っている水槽があります。
上の給水管Aからは毎分15Lの水が入り、下の排水管Bからは毎分40Lの水が出ていきます。
このとき次の問いに答えなさい。」
(1)水槽からは毎分何Lの水が出ていきますか?
(2)水槽が空になるまで何分かかりますか?
線分図の上側と下側の書き方を覚えましょう
【例題1 解説】
ニュートン算では2つの変化する数字が出てきます。
この問題では、給水管Aから入ってくる水量とBから出ていく水量ですね。
これらをしっかり区別して、図を書いていきます。
(1)
毎分出ていく水の量は、最初に入っていた500Lとは無関係なので、
(水が出ていく量)-(入ってくる量)
となります。
よって、
40-15=25L
となります。
(2)
水槽が空になるまでx分かかるとします。
そして、次の図の書き方をマスターしましょう。
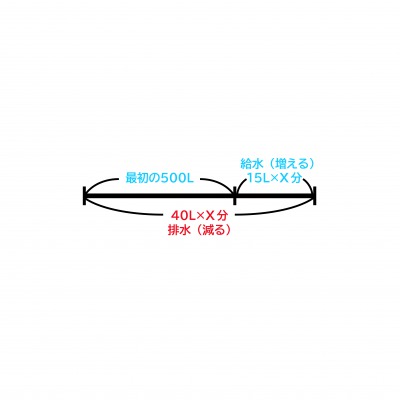
この線分図のポイントは、最初に入っていた水量と、増えていく水量は線分の上側に書くこと。そして、出ていく水量は線分の下側に書くことです。
この図では、最初の500Lとx分間に増える水の量の和が、同じx分間に出ていく量に等しくなり、図では同じ長さになっています。
そしてこの図が書けたら、あとは線分の文字が入っている部分に注目します。
線分の上には15×x、下には40×xがありますね。
この差は、
40×x-15×x=25×x
これが500Lに等しいので、
25×x=500…①
x=20
となり、答えは20分となります。
線分の上には、最初からある量と増える量、下には減らしていく量を書いてください。
そしてその差を取りましょう。
ちなみに(1)で毎分25Lの水が出ていくことを求めたので、それを使えば①式をすぐに出すことができます。
慣れてきたら、この問題は図がなくても解けるようになるでしょう。
それでは次の問題を見てみましょう。
時間が大事です!
【例題2】
「水族館の開演前に400人の来場者が並んでいます。
開演後も1分間に30人ずつお客さんが来ますが、窓口を2ヶ所開けると、40分で行列はなくなります。
このとき次の問いに答えなさい。」
(1)窓口1カ所で、1分間に何人のお客さんを入場させることができますか?
(2)窓口を4ヶ所開くと、何分で行列はなくなりますか?
【例題2 解説】
ニュートン算らしい、人が次々に押し寄せてくる問題ですね(笑)。
40分で行列がなくなるので、増える人数も減っていく人数もこれを使って求めることになります。
(1)
窓口1ヶ所で、1分間にx人のお客さんを入場させることができるとします。
例題1の考え方を使うと、図はこのようになります。
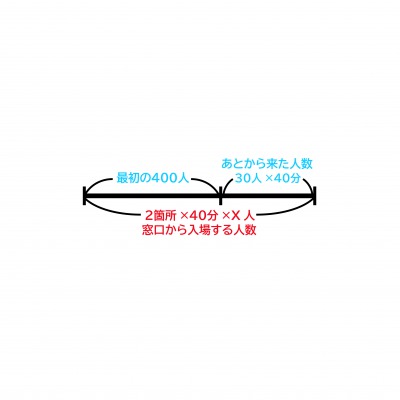
今回は最初に並んでいた400人と開園後40分間で増えた人数の和が、窓口2ヶ所で40分間で入場させることのできる人数に等しくなります。
それを式で表すと、
400+30×40=2×40×x
1600=80×x
x=20
よって窓口1ヶ所で1分間に入場できる人数は20人となります。
(1)と(2)のつながり
(2)
窓口4ヶ所で行列がなくなるまでにy分かかるとします。
図はこのようになります。
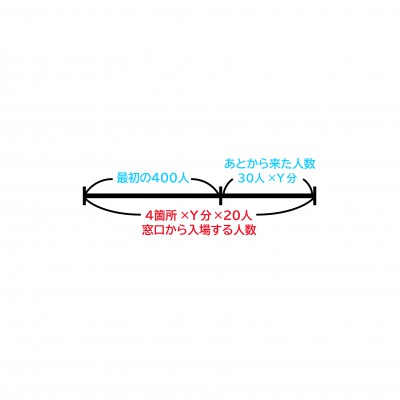
線分の下の式を、4×20としてしまいがちですが、(1)で求めた1分あたりに窓口から入場できる人数を必ずかけるようにしてください。
ニュートン算に限らず、算数では先の求めた答を次の問題でも使うことがよくありますよね。
そうするとこの図は【例題1】と同じで、文字が入った部分の差をとっていきます。
線分の上は30×y、下は80×yになるので、その差は、
80×y-30×y=50×y
これが線分上の400に等しいので、
50×y=400
y=8
よって8分となります。
図を書くための数値を一つ一つ、丁寧に求めていきましょう。
それでは最後の問題です。
線分図が2本!
【例題3】
「1時間に一定の割合て水が湧き出ている泉があります。
4台のポンプで水を汲み出すと5時間で泉は空になり、6台のポンプで汲み出すと3時間かかります。また、ポンプは1時間あたり20Lの水を汲み出すことができます。
このとき次の問いに答えなさい。」
(1)泉には1時間あたり何Lの水が湧き出ていますか?
(2)最初に泉にあった水は何Lですか?
差のとり方に注意!
【例題3 解説】
このニュートン算の問題では、2本の線分図の差のとり方がとても大切です。
最初に泉に入っていた水の量をxL、1時間あたり湧き出てくる量をyLとします。
ポンプ4台を使ったときと6台のときの図は、それぞれこのようになります。
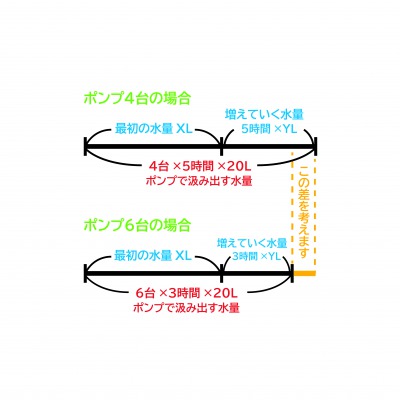
両方とも、1つの線分の中に2つの文字が入っていることに注意してください。
さて、ここでまた差をとっていきます。
そしてここが重要です。
これまで例題1、2では、1本の線分の上下の差を考えました。
しかしこの問題では、それぞれの線分の上側と上側、下側と下側を比べるのです!
つまり、4台のポンプを使った線分図の上側は、
x+5×y
6台のほうの図の上側は、
x+3×y
よってこの差は、
x+5×y-(x+3×y)=2×y
同様にして、それぞれの線分の下側の差は、
4×20×5-6×20×3=400-360=40
上下の差は等しくなるので、
2×y=40
y=20
以上から、泉には1時間あたり20Lの水が湧き出てくることになります。
ニュートン算らしい、独特な計算方法ですね。
(2)
y=20から、4台のポンプの図で考えると、
(線分の上側の水量)=x+5×20
(線分の下側の水量)=4×20×5
これらが等しいので、
x+5×20=4×20×5
x+100=400
x=300
ゆえに、最初に泉に入っていた水量は300Lとなります。
(1)で線分の上の部分の差をとったときに、最初に入っていた量xは相殺されるのがポイントです。
たくさん線分を書きましょう!
以上でニュートン算の解説はおしまいです。
最初は線分1本で解ける問題をしっかりとマスターしてください。
そして線分が2本必要な問題でも差をとることに変わりはありませんが、線分の上側と上側、下側と下側を比べることを忘れないようにしましょう。
おわりに
こちらの記事を読まれたお子さまへ
もしも勉強のことでお困りなら、親御さんに『アルファ』を紹介してみよう!

「勉強のやり方が分からない!」
「何から始めれば良いの??」
「前回のテストの点数、ちょっとやばかったな…」
そんなことでお困りではありませんか?
『家庭教師のアルファ』なら、あなたにピッタリの家庭教師がマンツーマンで勉強を教えてくれるので、
どんなに今の学力や成績に自信がなくても、着実に力を付けていくことがでいます!
もしも今、ちょっとでも家庭教師に興味があれば、ぜひ親御さんへ『家庭教師のアルファ』を紹介してみてください!
下のボタンから、アルファの紹介ページをLINEで共有できます!
こちらの記事をお読みいただいた保護者さまへ
さて、この記事をお読み頂いた方の中には
「中学受験をしようと思っているが、本当に合格できるか不安」
「受験を決断するのが遅かったので、もう間に合わないかも」
「進学塾に通わせているが、授業についていけないみたい…」
といった、中学受験に関するお悩みを持つ方も多いのではないでしょうか。
家庭教師のアルファが提供する完全オーダーメイド授業は、中学受験対策に最適です。
経験豊富なプロ家庭教師がマンツーマン授業を通じて、苦手な科目も細かく、丁寧に教えます。
アルファなら、お子様の学習状況や志望校に合った受験対策を行うことができますので、合格の可能性は極めて高くなります。
「もう6年生だけど、まともな対策が出来ていない」といった方も、まずはご相談ください。
アルファには、数ヵ月で志望校に合格した実績も数多くあります。
お子さまの中学受験についてお困りの方は、是非一度、アルファの指導を体験してみてください。下のボタンから、無料体験のお申込みが可能です。
こちらの記事の監修者

浅井保(あさい たもつ)
- ・北海道大学文学部卒
- ・家庭教師のアルファ 講師部長
2008年に『家庭教師のアルファ』のプロ家庭教師として活動開始し、数多くの生徒への学習指導を経験。
現在、株式会社アルファコーポレーション講師部部長。











