目次
ルート(√)って何？
ルート（√）は、「平方根」といいます。
ルートという記号の読み方は、「root」(根、という意味)からきています。
「平方」は、２乗、という意味ですので、２乗の根、ということです。
つまり、２乗すると根から成長して記号が外れる、という仕組みです。
２乗は同じ数字を掛けることですから、√２×√２＝２、ということになります。
また、－√２×（－√２）＝２です。
そして、２の平方根は、２乗すると２になる数なので、√２と－√２、になります。
ルートの計算方法・足し算引き算の仕方は？
ルートは、xやyやπと同じ扱いになるので、同じ仲間同士じゃないと計算できません。ルートの中の数が同じ時だけ、係数を足し算、引き算します。
例）√２+√２＝２√２
２√３+５√３＝７√３
２√５+√３－√５－４√３＝√５－３√３
８+√２－√２+√３＝８+√３
ルートの計算方法・掛け算割り算の仕方は？
掛け算、割り算は、ルート同士、係数同士をそのまま計算します。
例）３√２×５√３＝１５√６
４√２×√２＝４×２＝８
√１０×３√５＝３√５０←ルートの中が大きいので整理する必要あり（＜５＞参照）
６√６÷２√３＝３√２
√２÷√２＝１
５√１０÷√２＝５√５
ルートの掛け算をしていると、ルートの数が大きくなっていきます。ルートの中の数が大きくなってきたときは整理していく、というルールがあります。
ルートの数はどうやって整理するの？
ルートの中にある数は、２乗すればルートが外れます（＜２＞参照）。これを利用して、出来るだけルートの中の数は小さくして答える、という決まりがあります。
例）√５０＝√２×√５×√５になるので、√５０＝５√２とします。
√２８＝√２×√２×√７＝２√７
「素因数分解」という技を使えば、素数だけの掛け算に分解できるので、２乗のペアを見つけやすいです（全ての数は素数だけの掛け算の式で表せる！）。
これによって、掛け算も工夫してできるときもあります。
例）通常計算 √１２×√８＝√９６
√９６＝√２×√２×√２×√２×√２×√３＝４√６
工夫すると √１２＝２√３、 √８＝２√２
２√３×２√２＝４√６
だいぶすっきりした計算になりますね。
有理化、ってなに？
ルートの割り算を計算しているときに、割り切れず分数にすることがあります。
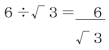
このように、分母にルートが残ったとき、分母のルートを外す作業を「有理化」といいます。解答するときに、分母にルートがあるときは有理化して答える、という決まりになっています。有理化の仕方は次のところで！
有理化、ってどうやるの？
有理化は、基本的に分母と同じ数を分母と分子、両方にかければ出来ます。
上下に同じ数字を掛けるので、１を掛けていることになりますね。
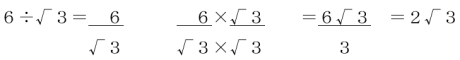
やっぱり解答は、出来るだけすっきりとした方がいいですよね。
分母に整数とルートが残ったときは、（ａ＋ｂ）（ａ－ｂ）＝a²－b²を利用します。
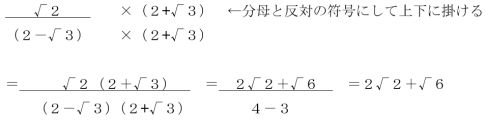
と、なります。
ルートって覚えた方がいいの？
学校などで√２＝１．４１４２１３５６、√３＝１．７３２０５０８、
√５＝２．２３６０６７９は習うかもしれません。しかし、実際にこの数値を使う必要がある問題には「√２＝１．４１４で計算せよ」などの表記があります。
しっかり理解しておく必要があるのは、例えば、√１１は３と４の間の数、ということです（３＝√９、４＝√１６。√１１はその間なので３．・・・の数）。
よくある問題で、「√６の整数部分をａ、小数部分をｂとする」というものがあります。
この場合、√６は２と３の間なので、整数部分は２、小数部分は整数部分の２を引いたものになるので、「√６－２」ということになります。
ルートの中はマイナスにはならないの？
ルートは、「２乗するとその数になる」という意味です。２乗すると必ずプラスになるので、
２乗してマイナスになる「√－２」のような数は存在しないことになります。
ただ、計算上そういう数があったほうが都合がよい、ということがあり、新たなルールとして「２乗すると－１になる数」を作り、それを「複素数」と呼んでいます。
複素数を含めた範囲で計算するときは√－２などでてくることがあります。
高校で習うことがあるかもしれませんね。
まとめ
ルートは、実際に計算してみると意外と難しくありませんし、計算の範囲が広がるので、辺の長さを算出できたり、手の届かない高さなども計算できたりします。
高校数学では必須になりますので、計算練習をしっかりして、自分のものにしていきましょう。
こちらの記事を読まれたお子さまへ
もしも勉強のことでお困りなら、親御さんに『アルファ』を紹介してみよう！
「勉強のやり方が分からない！」
「何から始めれば良いの？？」
「前回のテストの点数、ちょっとやばかったな…」
そんなことでお困りではありませんか？
『家庭教師のアルファ』なら、あなたにピッタリの家庭教師がマンツーマンで勉強を教えてくれるので、
どんなに今の学力や成績に自信がなくても、着実に力を付けていくことがでいます！
もしも今、ちょっとでも家庭教師に興味があれば、ぜひ親御さんへ『家庭教師のアルファ』を紹介してみてください！
下のボタンから、アルファの紹介ページをLINEで共有できます！
こちらの記事をお読みいただいた保護者さまへ
さて、この記事をお読み頂いた方の中には
「子どもが中学生になってから苦手な科目が増えたみたい」
「部活が忙しくて勉強する時間がとれない」
「このままだと高校受験が心配」
といった、お子さまの勉強に関するお悩みを持たれている方も多いのではないでしょうか。
中学生は授業のペースがどんどん早くなっていき、単元がより連鎖してつながってきます。
そのため、一つの単元につまづいてしまうと、そこから連鎖的に苦手意識が広がってしまうケースが多いのです。
したがって、一つ一つの単元を確実に理解しながら進めることが大切になってきます。
口で言うのは簡単ですが、これがなかなか、一人で行うのは難しいもの。
家庭教師のアルファが提供する完全オーダーメイド授業は、一人ひとりのお子さまの状況を的確に把握し、学力のみならず、性格や生活環境に合わせた指導を行います。もちろん、受験対策も志望校に合わせた対策が可能ですので、合格の可能性も飛躍的にアップします。
中学生のお子さまの勉強についてお困りの方は、是非一度、プロ家庭教師専門のアルファの指導を体験してみてください。下のボタンから、無料体験のお申込みが可能です。
こちらの記事の監修者
浅井保(あさい たもつ)
・北海道大学文学部卒
・家庭教師のアルファ 講師部長
・山手中央高等学院 学院長
2008年に『家庭教師のアルファ』のプロ家庭教師として活動開始。
現在、株式会社アルファコーポレーション講師部部長、および同社の運営する通信制サポート校・山手中央高等学院の学院長を兼務しながら講師として指導にも従事。
