目次
確率の定義

確率の定義とはと聞かれるとわからない人が多いと思います。
なぜなら定義は中学時代に軽く触れるだけでなんとなくで中学時代の確率をこなしてしまっているからなのです。
ここで改めて確率の定義について解説します。
確率の定義とは、全事象U、事象Aの要素の個数をそれぞれn(U)、n(A)とする。
全事象Uの根元事象が同様に確からしいとき、事象Aの起こる確率P(A)は以下の式になる。
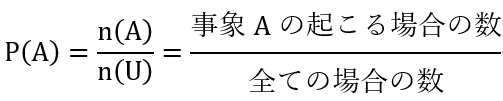
この定義さえ理解していれば確率が理解できるようになると思います。
さらに確率の計算をするときは同じものでも区別する必要があります。
例)赤が3つある場合は、赤1、赤2、赤3のように区別しなければならない。
では実際に解説しながら問題を解いていきましょう。
サイコロを使った確率
サイコロの確率問題では起こりうる全ての場合の数は常に6nで表現することが
でき、nはサイコロの個数を当てはめて計算します。
サイコロの問題での難しく感じるポイントは2つのサイコロを区別するかしないかがわからないからです。日本語の問題文を確認して区別するかしないかさえわかれば簡単に解けるようになります。
では問題を解いてみましょう。
大小2つのサイコロを投げるとき、目の和が5になる確率を求めなさい。
〜ポイント〜
大小の言葉でこの問題が区別する問題であることがわかります。
そのため大きいサイコロの出目をA、小さいサイコロの出目をBとして計算していきます。
〜解説〜
まず起こりうる全ての場合の数2つのサイコロを用いるので6²通りになります。
次に今回の事象Aつまり目の和が5になる場合の数は(1,4)(2,3)(3,2)(4,1)になります。これらの数は1と4の組み合わせ、2と3の組み合わせなのでそれぞれ2!通りになります。
これらを整理すると
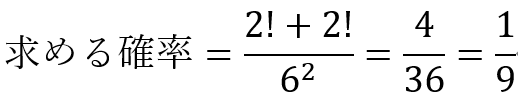
となります。
コインを使った確率
コインを使った確率の問題では表が出る確率と裏が出る確率は共に1/2である。
そのため起こりうる全ての場合の数は2nで表現することができ、nはコインの投げた回数を当てはめて計算します。
コインの問題では反復試行の確率と特定の回数が出る確率の2つのパターンの問題が多いのでその2つの問題の解いてみましょう。
まずは反復試行の問題です。
コインを同時に3枚投げたとき、全て表となる確率を求めよ。
〜ポイント〜
まず全ての場合を考え出しましょう。
表表表、表表裏、表裏表、裏表表、表裏裏、裏表裏、裏裏表、裏裏裏
〜解説〜
コインを3枚同時に投げた時の起こりうる全ての場合の数は2³なので8となる。
その中で表表表のパターンは1つなので確率は1/8となる。
次に特定の回数が出る確率の問題です。
コインを3枚投げた時2回表が出る確率を求めよ。
〜ポイント〜
3回の中で2回の表が出る確率は³C²通りで表すことができる。
〜解説〜
コインを3枚同時に投げた時の起こりうる全ての場合の数は2³なので8となる。
その中で3回投げた時に2回表が出るのは³C²なので3となる。
2つの事から確率は3/8であるといえる。
袋と玉を使った確率
袋と玉の確率では、起こりうる全ての場合の数は袋の中にある玉を無条件に取り出すことをしましているのでコンビネーションを用いて表現します。
起こりうる全ての場合の数=袋の中の玉の数 C 取り出したい玉の数となります。
袋と玉の確率少し大変な部分は同時にとる、玉を戻さず取る、球を戻して取るの3つのパターンが同じような問題でもやっていることが違ってくるのです。
そこで3つのパターンの問題の解いてみましょう。
まずは玉を同時にとる場合です。
赤玉4個白玉3個入ってる袋の中から玉を2個取り出す時、取り出した玉が赤玉と白玉である確率を求めよ。
〜ポイント〜
赤玉4個の中1つ取り出す確率と白玉3個の中から1つ取り出す確率を求めましょう。

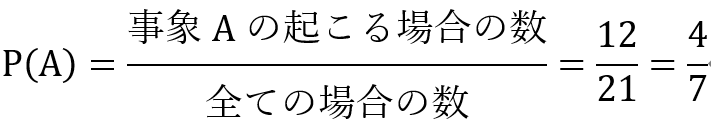
次に玉を戻して取る場合です。
赤玉4個白玉3個入ってる袋の中から玉を1個ずつ取る時、取った玉を戻さずに白-白-赤の順で玉が出る確率を求めよ。
〜ポイント〜
玉を戻さないということは常に袋の中の玉の数は変化するという事になるのでそこが注意です。
〜解説〜
まずは1回目に白が出る確率は3/7で表現できます。
次に2回目に白が出る確率は袋の中の玉の数は1回目の玉の分の1つ少なくります。
なので2回目に白が出る確率は2/6で表現できます。
最後に3回目に赤が出る確率は袋の中の玉の数が1回目と2回目の玉の分の2つ少なくなります。
なので3回目に赤が出る確率は4/5で表現できます。
これらの事象の全てが同時に起こり得るのが今回求めたい確率なので3つの事象を掛け合わせることで全体の事象の確率を求めることができるのでこのようになります。
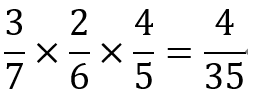
最後に取り出した玉を戻す場合です。
赤玉4個白玉3個入ってる袋の中から玉を1個ずつ取る時、取った玉を袋に戻し、白-白-赤の順で玉が出る確率を求めよ。
〜ポイント〜
取った玉を袋に戻すということは常に袋の中の玉の数は変わらないのが戻さない問題との違いです。
〜解説〜
まずは1回目に白が出る確率は3/7で表現できます。
次に2回目に白が出る確率は袋の中の玉の数は1回目の玉は戻すので袋の中の玉の数は変わらないので2回目に白が出る確率も3/7で表現できます。
最後に3回目に赤が出る確率も袋の中の玉の数はかわらないので3回目に赤が出る確率は4/7で表現できます。
これらの事象の全てが同時に起こり得るのが今回求めたい確率なので3つの事象を掛け合わせることで全体の事象の確率を求めることができるのでこのようになります。
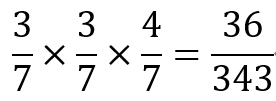
まとめ
数学はやればやるだけしっかりと身につきます。
毎日コツコツ理解していければ必ず結果に繋がります。
今回は確率の基本的な問題の解き方について解説しました。
確率の難しく感じる点はしっかり問題文を読まないといけないということだと思います。
ですが問題文をしっかり読み想像ができるようになれば問題も簡単に見えてきます。
受験にも大きく影響する範囲なのでしっかり抑えていきましょう。
おわりに
こちらの記事を読まれたお子さまへ
もしも勉強のことでお困りなら、親御さんに『アルファ』を紹介してみよう!

「勉強のやり方が分からない!」
「何から始めれば良いの??」
「前回のテストの点数、ちょっとやばかったな…」
そんなことでお困りではありませんか?
『家庭教師のアルファ』なら、あなたにピッタリの家庭教師がマンツーマンで勉強を教えてくれるので、
どんなに今の学力や成績に自信がなくても、着実に力を付けていくことがでいます!
もしも今、ちょっとでも家庭教師に興味があれば、ぜひ親御さんへ『家庭教師のアルファ』を紹介してみてください!
下のボタンから、アルファの紹介ページをLINEで共有できます!
こちらの記事をお読みいただいた保護者さまへ
さて、この記事をお読み頂いた方の中には
「子どもが中学生になってから苦手な科目が増えた」
「部活が忙しくて勉強する時間がとれない」
「このままだと高校受験が心配」
といった、お子さまの勉強に関するお悩みを持たれている方も多いのではないでしょうか。
中学生は授業のペースがどんどん早くなっていき、単元がより連鎖してつながってきます。
そのため、一つの単元につまづいてしまうと、そこから連鎖的に苦手意識が広がってしまうケースが多いのです。
したがって、一つ一つの単元を確実に理解しながら進めることが大切になってきます。
口で言うのは簡単ですが、これがなかなか、一人で行うのは難しいもの。
家庭教師のアルファが提供する完全オーダーメイド授業は、一人ひとりのお子さまの状況を的確に把握し、学力のみならず、性格や生活環境に合わせた指導を行います。もちろん、受験対策も志望校に合わせた対策が可能ですので、合格の可能性も飛躍的にアップします。
中学生のお子さまの勉強についてお困りの方は、是非一度、プロ家庭教師専門のアルファの指導を体験してみてください。下のボタンから、無料体験のお申込みが可能です。
こちらの記事の監修者

浅井保(あさい たもつ)
- ・北海道大学文学部卒
- ・家庭教師のアルファ 講師部長
2008年に『家庭教師のアルファ』のプロ家庭教師として活動開始し、数多くの生徒への学習指導を経験。
現在、株式会社アルファコーポレーション講師部部長。











