方程式とは?
さて、問題です。
次の□に入る数はなんでしょうか?
【例1】
□+2=3
もちろんわかりましたね?
正解は「1」です。
ここで中学生らしく、□をxに代えて書き直すと、
x+2=3…(1)
x=1
となります。
文字を使って書くと難しそうに見えますが、□を使っていたのをxに置き換えただけなので、あまり身構えないでください。
(1)式のように、不明な文字を含む等式(=で結ばれた式)を「方程式」といい、その文字の値をもとめることを「方程式を解く」といいます。
さて、【例1】は、
□と2を足したら3になる→□は1
のように、中学の知識に関係なく解けたと思います。
中学ではこの問題を次のように解きます。
(□はxとします)
【例1】の解き方(中学生バージョン)
x+2=3
両辺から2を引くと、
x+2-2=3-2
x=1
「式が長い!」と思った方もいることでしょう(笑)。
これは「等式の性質」を利用して解いたもので、等式には次の4つの性質があります。
【等式の性質】
1,等式の両辺に同じ数を足しても、等式は成り立つ
2,等式の両辺から同じ数を引いても、等式は成り立つ
3,等式の両辺に同じ数をかけても、等式は成り立つ
4,等式の両辺を同じ数で割っても、等式は成り立つ
等式の「=」の左側を左辺、右側を右辺、そして2つをあわせて両辺といいます。
【例1】の解き方で、両辺から2を引いたのは、等式の性質2を利用したものです。
方程式では最終的に「x=数字」の形にするので、最初に左辺にあった「+2」を消すために「-2」をつけました。
このとき、必ず右辺にも「-2」をつけます。
このように等式の性質を利用する際は、両辺に同じ計算をつけ加えることを忘れないでください。
それでは等式の性質1~4を順番に使ってみましょう。
【例2】
次の方程式を解きなさい。
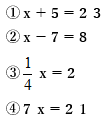
【例2】の解答
等式の性質1~4を順番に利用していきます。
①両辺から5を引くと、
x+5-5=23-5
x=18
②両辺に7を足すと、
x-7+7=8+7
x=15
③両辺に4をかけると、
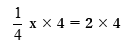
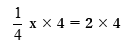
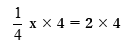
x=8
④両辺を7で割ると、
7x÷7=21÷7
x=3
③のようにxの係数が分数になると間違えやすくなります。
その際は分母と同じ数を両辺にかけて、分数をなくしてから計算を進めましょう。
【移項とは?】
さて、【例2】①の問題と解答を、もう一度見てください。
①x+5=23
x+5-5=23-5
x=18
2行目の左辺のみ計算すると、xになりますね。
つまりこの式は、次のように書き換えることもできます。
①x+5=23
x=23-5
x=18
これは「移項」という計算方法を使ったもので、1行目の左辺の「+5」を、2行目では右辺に移動して「-5」になっています。
移項では、「=」を飛び越えて左辺から右辺に、あるいは右辺から左辺に数字や文字を移動した際は、符号を変えることになります。
等式の性質①、②をそのまま利用するよりは、書く分量が減るので覚えておきましょう。
それでは移項と等式の性質③、④を使っていきましょう。
【例3】
次の方程式を解きなさい。
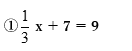
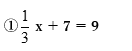
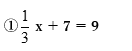
②5x+23=3x+9
【例3】の解答
①7を右辺に移項すると、
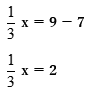
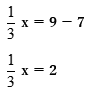
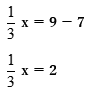
両辺に3をかけると、



②3xを左辺に、23を右辺に移項すると、
5x-3x=9-23
2x=-14
両辺を2で割ると、
2x÷2=-14÷2
x=-7
【かっこがついた方程式】
方程式の文章題でよく登場しますが、かっこのついた式は、かっこを展開してから解いきます。
【例4】
次の方程式を解きなさい。
①2(x+4)=16
②5x+3=7(x+5)
【例4】の解答
①左辺を展開すると、
2x+8=16
2x=16-8
2x=8
x=4
②右辺を展開すると、
5x+3=7x+35
5x-7x=35-3
-2x=32
x=-16
かっこを展開する際は、かっこの中のすべての項にかけ算をすることを忘れないようにしましょう。
【両辺に小数や分数の項があるとき】
さて、ここまで来れば方程式の計算マスターまであと一歩です。
【例5】
次の方程式を解きなさい。
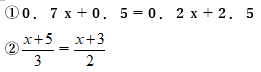
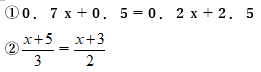
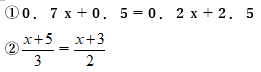
小数の項が両辺にある場合は、両辺に10や100をかけて、すべての項を整数にしてから計算します。
また、両辺に分数がある場合は、分母の最小公倍数を両辺にかけましょう。
【例5】の解答
①両辺に10をかけると、
(0.7x+0.5)×10=(0.2x+2.5)×10
7x+5=2x+25
7x-2x=25-5
5x=20
x=4
②両辺に3と2の最小公倍数の6をかけると、
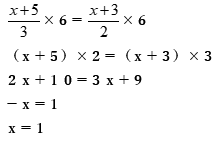
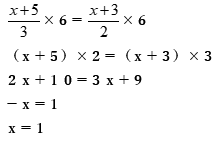
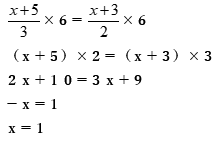
【おわりに】
方程式の計算問題の説明は以上です。
数学はスポーツと同じで、例を見たあとに自分で問題を解いて計算方法を身につけていくものです。
問題に応じて等式の性質が反射的に出てくるまで、解いて解いて解きまくりましょう!
等式の性質
さて、【例1】は、
□と2を足したら3になる→□は1
のように、中学の知識に関係なく解けたと思います。
中学ではこの問題を次のように解きます。
(□はxとします)
【例1】の解き方(中学生バージョン)
x+2=3
両辺から2を引くと、
x+2-2=3-2
x=1
「式が長い!」と思った方もいることでしょう(笑)。
これは「等式の性質」を利用して解いたもので、等式には次の4つの性質があります。
【等式の性質】
1,等式の両辺に同じ数を足しても、等式は成り立つ
2,等式の両辺から同じ数を引いても、等式は成り立つ
3,等式の両辺に同じ数をかけても、等式は成り立つ
4,等式の両辺を同じ数で割っても、等式は成り立つ
等式の「=」の左側を左辺、右側を右辺、そして2つをあわせて両辺といいます。
【例1】の解き方で、両辺から2を引いたのは、等式の性質2を利用したものです。
方程式では最終的に「x=数字」の形にするので、最初に左辺にあった「+2」を消すために「-2」をつけました。
このとき、必ず右辺にも「-2」をつけます。
このように等式の性質を利用する際は、両辺に同じ計算をつけ加えることを忘れないでください。
それでは等式の性質1~4を順番に使ってみましょう。
【例2】
次の方程式を解きなさい。
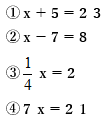
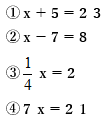
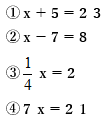
【例2】の解答
等式の性質1~4を順番に利用していきます。
①両辺から5を引くと、
x+5-5=23-5
x=18
②両辺に7を足すと、
x-7+7=8+7
x=15
③両辺に4をかけると、
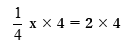
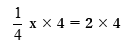
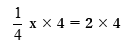
x=8
④両辺を7で割ると、
7x÷7=21÷7
x=3
③のようにxの係数が分数になると間違えやすくなります。
その際は分母と同じ数を両辺にかけて、分数をなくしてから計算を進めましょう。
【移項とは?】
さて、【例2】①の問題と解答を、もう一度見てください。
①x+5=23
x+5-5=23-5
x=18
2行目の左辺のみ計算すると、xになりますね。
つまりこの式は、次のように書き換えることもできます。
①x+5=23
x=23-5
x=18
これは「移項」という計算方法を使ったもので、1行目の左辺の「+5」を、2行目では右辺に移動して「-5」になっています。
移項では、「=」を飛び越えて左辺から右辺に、あるいは右辺から左辺に数字や文字を移動した際は、符号を変えることになります。
等式の性質①、②をそのまま利用するよりは、書く分量が減るので覚えておきましょう。
それでは移項と等式の性質③、④を使っていきましょう。
【例3】
次の方程式を解きなさい。
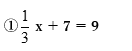
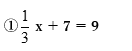
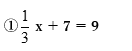
②5x+23=3x+9
【例3】の解答
①7を右辺に移項すると、
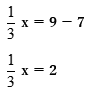
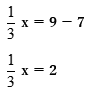
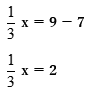
両辺に3をかけると、



②3xを左辺に、23を右辺に移項すると、
5x-3x=9-23
2x=-14
両辺を2で割ると、
2x÷2=-14÷2
x=-7
【かっこがついた方程式】
方程式の文章題でよく登場しますが、かっこのついた式は、かっこを展開してから解いきます。
【例4】
次の方程式を解きなさい。
①2(x+4)=16
②5x+3=7(x+5)
【例4】の解答
①左辺を展開すると、
2x+8=16
2x=16-8
2x=8
x=4
②右辺を展開すると、
5x+3=7x+35
5x-7x=35-3
-2x=32
x=-16
かっこを展開する際は、かっこの中のすべての項にかけ算をすることを忘れないようにしましょう。
【両辺に小数や分数の項があるとき】
さて、ここまで来れば方程式の計算マスターまであと一歩です。
【例5】
次の方程式を解きなさい。
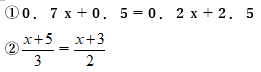
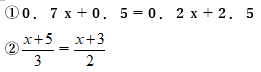
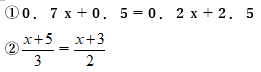
小数の項が両辺にある場合は、両辺に10や100をかけて、すべての項を整数にしてから計算します。
また、両辺に分数がある場合は、分母の最小公倍数を両辺にかけましょう。
【例5】の解答
①両辺に10をかけると、
(0.7x+0.5)×10=(0.2x+2.5)×10
7x+5=2x+25
7x-2x=25-5
5x=20
x=4
②両辺に3と2の最小公倍数の6をかけると、
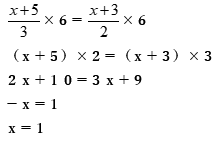
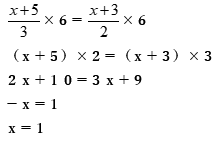
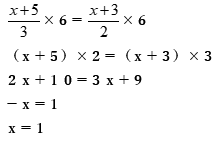
【おわりに】
方程式の計算問題の説明は以上です。
数学はスポーツと同じで、例を見たあとに自分で問題を解いて計算方法を身につけていくものです。
問題に応じて等式の性質が反射的に出てくるまで、解いて解いて解きまくりましょう!
なお、一次方程式の解き方については、アルファの公式YouTubeチャンネル「超かんたん!勉強チャンネル」でも、計6つの動画に分けて解説しています。
そちらもぜひご覧ください。
こちらの記事を読まれたお子さまへ
もしも勉強のことでお困りなら、親御さんに『アルファ』を紹介してみよう!


「勉強のやり方が分からない!」
「何から始めれば良いの??」
「前回のテストの点数、ちょっとやばかったな…」
そんなことでお困りではありませんか?
『家庭教師のアルファ』なら、あなたにピッタリの家庭教師がマンツーマンで勉強を教えてくれるので、
どんなに今の学力や成績に自信がなくても、着実に力を付けていくことがでいます!
もしも今、ちょっとでも家庭教師に興味があれば、ぜひ親御さんへ『家庭教師のアルファ』を紹介してみてください!
下のボタンから、アルファの紹介ページをLINEで共有できます!
こちらの記事をお読みいただいた保護者さまへ
さて、この記事をお読み頂いた方の中には
「中学生になってから苦手な科目が増えた」
「部活が忙しくて勉強する時間がとれない」
「このままだと高校受験が心配」
といった、お子さまの勉強に関するお悩みを持たれている方も多いのではないでしょうか。
中学生は授業のペースがどんどん早くなっていき、単元がより連鎖してつながってきます。
そのため、一つの単元につまづいてしまうと、そこから連鎖的に苦手意識が広がってしまうケースが多いのです。
したがって、一つ一つの単元を確実に理解しながら進めることが大切になってきます。
口で言うのは簡単ですが、これがなかなか、一人で行うのは難しいもの。
家庭教師のアルファが提供する完全オーダーメイド授業は、一人ひとりのお子さまの状況を的確に把握し、学力のみならず、性格や生活環境に合わせた指導を行います。もちろん、受験対策も志望校に合わせた対策が可能ですので、合格の可能性も飛躍的にアップします。
中学生のお子さまの勉強についてお困りの方は、是非一度、プロ家庭教師専門のアルファの指導を体験してみてください。下のボタンから、無料体験のお申込みが可能です。
こちらの記事の監修者

浅井保(あさい たもつ)
- ・北海道大学文学部卒
- ・家庭教師のアルファ 講師部長
2008年に『家庭教師のアルファ』のプロ家庭教師として活動開始し、数多くの生徒への学習指導を経験。
現在、株式会社アルファコーポレーション講師部部長。











