等加速度直線運動について｜高校生／物理

目次

• 等加速度直線運動の3つの公式
• 例題1
• 例題2

等加速度直線運動の3つの公式

「等加速度直線運動」についてです。高校科目は「物理基礎」です。
等加速度直線運動とは、一定の加速度aで直線上を運動することです。
例えば、高い建物の屋上から静かにボールを落とすときのボールの動きが、この運動です。

その公式は3つあります。

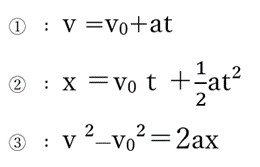
文字(物理量)の説明です。
t[s] : 時刻(時間)、v₀[m/s] (←ブイゼロと読む) : 初速度、a[m/s²] : 加速度(単位はメートル毎秒毎秒と読む)、v[m/s] : 時刻tでの速度、x[m] : 位置。
単位はmがメートル、sが秒です。
あと、時刻tは0以上、残りの文字は正負0どれもありです。
正負(符号)の決め方は原則vやv0から決めて、残りの文字もv₀などの正負と同じです。
問題に指定されていることもあります。

(参考)位置、速度、加速度のように、向きと大きさをもつ量を「ベクトル(量)」また、時間のように、数字だけの量を「スカラー(量)」といいます。
速度(←ベクトル量)の大きさが「速さ(←スカラー量)」です。数学、物理では速度と速さは区別します。

等加速度運動①②③の公式ですが、③は①②からtを消去して整理すれば導けます。
問題で、時刻が与えられていないときは③を使ったほうが良いです。
しかし、a、xの符号には注意して下さい。①②の式を立ててtを消去してもOKです。

例題1

■例題1
次の等加速直線運動をする物体の加速度の大きさは、それぞれ何m/s²か。

(1)静止していた物体が、動き出してから5.0s後に速度が20m/sになった。

(考え方)「静止していた」→「初速度v₀=0」、あと与えられている量が、時間(5s)、速度(20m/s)より、公式①を使います。
①のaの符号は、速度と同じです。

(解答)求める加速度をaと置き、等加速運動の公式①に、v=20、t=5、v₀=0を代入すると、
20=0+a×5、a=4.0
(答え)4.0m/s²
(注意)本当は「有効数字」の注意点があるのですが今回は省略します。(分かる人は、5.0より有効数字2桁で答えましょう。)

(2)静止していた物体が、動き出してから4.0s間に12mすすんだ。

(考え方)「12m、4s」→位置、時間から公式②を使う。「静止していた」→「v₀=0」、あと、x=12、t=4を代入する。

(解答)求める加速度をaと置き、等加速運動の公式②に、v₀=0、t=4、x=12 を代入すると、


(答え)1.5m/s²

(3)静止していた物体が、動き出してから8.0m進んだところで速さが4.0m/sになった。

(考え方)問題に「時間」が書いていない→等加速度運動の公式③を使う。「静止していた」→「v₀=0」、あと③で、v=4、x=8を代入する。

(解答)求める加速度をaと置き、公式③で、v₀=0、v=4、x=8を代入すると、
4²－0²=2×a×8、 a=1.0
(答え)1.0m/s²

例題2

■例題2
一直線上を10m/sの速さで走っている車が、一定の加速度で速さを増し、25m進んだところで15m/sの速さになった。
加速度の大きさは何m/s²か。

(考え方)「一定の加速度」→「等加速度運動の公式」が使える。
「問題に時間が書いていない」→「公式③を使う。」(①②を使ってもよい)
③にv₀=10、v=15、x=25を代入する。「速さを増し」→「a>0」

(解答)求める加速度をa(>0)として、等加速度運動の公式③を使う。③に、v₀=10、v=15、x=25を代入すると、
15²－10²=2×a×25、a=2.5
(答え)2.5m/s²

○今回は数字を正の数ばかりにしましたが、速度、加速度で数字が負の数なら向きは反対です。図を使った問題もあります。