漸化式の解き方｜高校生／数学

目次

• 漸化式って何？
• 漸化式の基本の３パターンの解き方
• 特性方程式の利用
• 漸化式が分数のときの特性方程式の利用
• 隣接３項間の漸化式の解き方
• まとめ

漸化式って何？

まず漸化式とはなんなのかということからお話ししたいと思います。
漸化式の意味は、数列の各項をその前の頃から1通りに定める規則を表す等式のことです。
難しい言葉に感じますが詳しく解説すると、
の２つの条件を満たしている場合にこれらの情報を用いてa₁,a₂,a₃,…の値が1つに定まる条件式のことを漸化式と呼びます。
まずは基本的な漸化式から学習していきましょう。

次の条件によってよって定められる数列の第2項から第5項を求めよ。

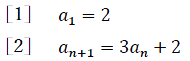
〜解説〜
第2項、第３項、第４項、第５項はそれぞれ𝑎₂,𝑎₃,𝑎₄,𝑎₅で表すことが出来る。
第１項は𝑎₁=2
第２項は［2］の式を𝑎_n=𝑎₁と考えて計算を行うことで求めることが出来る。
つまり𝑎₂=3×2+2=8となる。
第３項は［2］の式を𝑎_n=𝑎₂と考えて計算を行うことで求めることが出来る。
つまり𝑎₃=3×8+2=26となる。
第４項、第５項も同様に計算すると
第４項は𝑎₄=3×26+2=80
第５項は𝑎₅=3×80+2=242となります。

漸化式の基本の３パターンの解き方

漸化式の基本のパターンは3パターンとは



以上の３つの漸化式のことを指します。
これらの公式を用いた一般項の解き方を１つずつ解説していきたいと思います。

①等差数列型の漸化式の解き方
等差数列型の漸化式を用いる前にまずは等差数列の一般項の公式を思い出しておきましょう。
等差数列の一般項はで求めることができました。
漸化式では初項と公差を求めることができ、それを用いて基本の等差数列の一般項の公式を解くことで一般項を求めることができます。
それでは、実際に問題を解いてみましょう。

＜問題＞

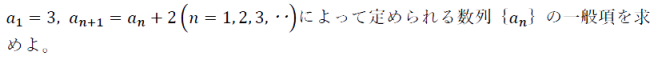
〜解説〜
まずは等差数列型の公式を用いて公差を求めましょう。

この式を、等差数列型の式の形に変形しましょう。

これにより初項が3公差が2の等差数列なので一般項は

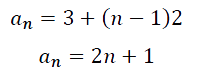
となります。

② 等比数列型の漸化式の解き方
等比数列型の漸化式を用いる前にまずは等比数列の一般項の公式を思い出しておきましょう。
等比数列の一般項はで求めることができました。
漸化式では初項と公比を求めることができ、それを用いて基本の等比数列の一般項の公式を解くことで一般項を求めることができます。
それでは、実際に問題を解いてみましょう。
＜問題＞

〜解説〜
まずは等比数列型の公式を用いて公比を求めましょう。

この式を、等比数列型の式の形に変形しましょう。

これにより初項が２公比が−３の等比数列なので一般項は
となります。

③ 階差数列型の漸化式の解き方
階差数列型の漸化式を用いる前にまずは階差数列の一般項の公式を思い出しておきましょう。
階差数列の一般項は

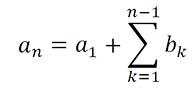
で求めることができました。
漸化式では初項と公比を求めることができ、それを用いて基本の等比数列の一般項の公式を解くことで一般項を求めることができます。
それでは、実際に問題を解いてみましょう。
＜問題＞

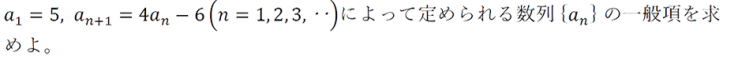
〜解説〜


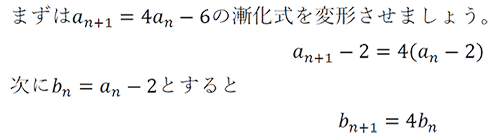
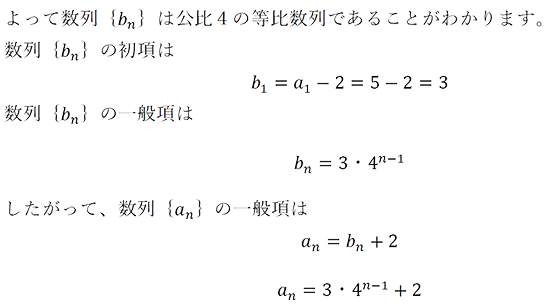
となります。
階差数列の漸化式の計算では特性方程式と呼ばれる計算方法をとることで1つ目の式の変形が可能になります。
ではその特性方程式がどういったものなのか少し説明しましょう。

特性方程式の利用

特性方程式とは
漸化式を簡単に解くための必要な値を求めることが出来る方程式のことです。

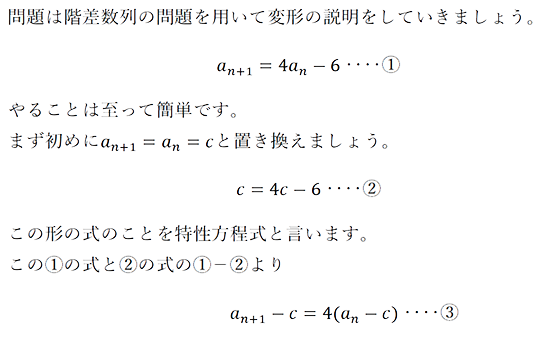
が成り立ちます。
この形の式のことを特性方程式と言います。
次にcについて計算しましょう。

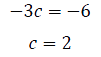
なので③の式のcに2を代入すると、

となりここからは階差数列の漸化式を求める流れに沿って進めることができます。さらに特性方程式は様々な場面で用いられることが多いです。
他の漸化式のパターンについてもいくつか学習しておきましょう。

漸化式が分数のときの特性方程式の利用

＜問題＞

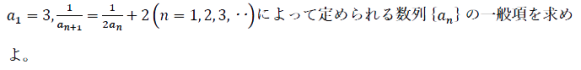
〜解説〜

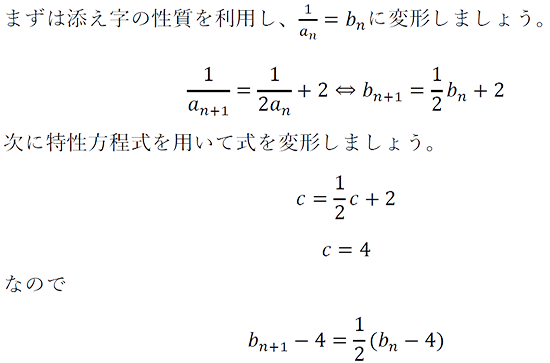
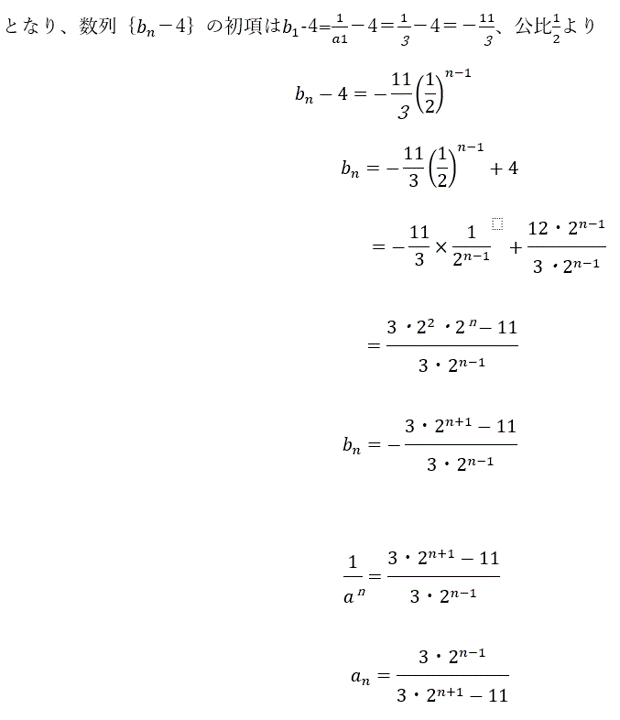
隣接３項間の漸化式の解き方

これまで解説してきたのは隣接する２項間の漸化式について求めてきました。
しかし隣接した３項間の漸化式と𝑎₁，𝑎₂によって数列が定められることもあります。
そこで、このような数列の一般項の求め方について解説していきましょう。
＜問題＞

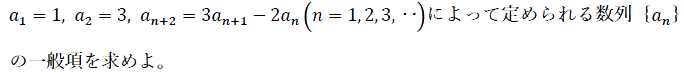
まずは漸化式を変形していきます。

となります。

まとめ

漸化式は受験対策をする上で必ず学習しなければならない重要な範囲です。
大学受験での出題率も非常に高いです。
漸化式を利用した一般項の求め方は必ずマスターしておきましょう。
まだまだ紹介しきれていない複数のパターンが存在しています。分類分けを間違わないようにしっかりと注意しながら進めていきましょう。

こちらの記事を読まれたお子さまへ
もしも勉強のことでお困りなら、親御さんに『アルファ』を紹介してみよう！

「勉強のやり方が分からない！」
「何から始めれば良いの？？」
「前回のテストの点数、ちょっとやばかったな…」

そんなことでお困りではありませんか？
『家庭教師のアルファ』なら、あなたにピッタリの家庭教師がマンツーマンで勉強を教えてくれるので、
どんなに今の学力や成績に自信がなくても、着実に力を付けていくことがでいます！

もしも今、ちょっとでも家庭教師に興味があれば、ぜひ親御さんへ『家庭教師のアルファ』を紹介してみてください！
下のボタンから、アルファの紹介ページをLINEで共有できます！

こちらの記事をお読みいただいた保護者さまへ

さて、この記事をお読み頂いた方の中には
「子どもが高校生になってから苦手な科目が増え、成績も落ち始めたみたい」
「部活が忙しくて勉強する時間がとれない」
「このままだと大学受験が心配」
といった、お子さまの勉強に関するお悩みを持たれている方も多いのではないでしょうか。
高校生は中学生に比べ学習量が圧倒的に多くなり、勉強の難度も上がるため、一気に挫折してしまうお子さまも多いのです。

高校生の効率的な成績向上・受験対策を行うには、現在の到達度を分析し、お子さまの状況にあわせた学習を行う必要があります。
ただ、お子さま一人で自身の現状を分析し、学習カリキュラムを組み上げるのは困難な場合がほとんどです。

家庭教師のアルファが提供する完全オーダーメイド授業は、一人ひとりのお子さまの状況を的確に把握し、学力のみならず、性格や生活環境に合わせた指導を行います。もちろん、受験対策も志望校に合わせた対策が可能ですので、合格の可能性も飛躍的にアップします。特に大学受験の場合、早い段階から学習カリキュラムを立て、計画的に対策を進める必要があるので、家庭教師は良きプランナーとしての役割も果たします。
高校生のお子さまの勉強についてお困りの方は、是非一度、プロ家庭教師専門のアルファの授業を体験してみてください。下のボタンから、無料体験のお申込みが可能です。

こちらの記事の監修者

　浅井保(あさい たもつ)
・北海道大学文学部卒
・家庭教師のアルファ 講師部長
・山手中央高等学院　学院長

　
2008年に『家庭教師のアルファ』のプロ家庭教師として活動開始。
現在、株式会社アルファコーポレーション講師部部長、および同社の運営する通信制サポート校・山手中央高等学院の学院長を兼務しながら講師として指導にも従事。