目次
解き方のコツは以下の二点!
ポイント①:グラフは必ず軸を中心に左右対称
ポイント②:頂点(軸)に遠いほど、間隔は広い。
→軸から遠いx座標ほど、y座標の値が大きくなる。(a>0のとき)
また、a<0の場合は、大小関係が反対になるため、以下のようになる。
軸から遠いx座標ほど、u座標の値が小さくなる。
この大小関係は、全て覚えるのではなく、1つを覚えて、大小を入れ替えていきましょう。
つまり、軸を中心にグラフの形を作ればよく、軸の位置さえ決めれば、グラフも不要です。
以下の問題で確認してみましょう
例1 f(x)=x²-4x+6のグラフの変域が次の場合のとき、それぞれの最大値と最小値を求めましょう。
(ア)-2≦x≦3 (イ)-2≦x≦1
解き方
まず、最初に必ず軸を求めましょう。このとき、平方完成を使うのも正解ですが

でもとめると時間も短縮できます。
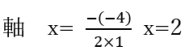
が軸となります。
(ア)の場合、-2≦2≦3となり、下向きのグラフのため、軸のy座標が最小値です。
最小値f(2)=2²-4×2+6=2
また、x=2において、x=-2のほうが x=3よりも遠いため、
最大値f(-2)=(-2) ²-4×(-2)+6=18
(イ) の場合、-2≦x<1の範囲には、軸x=2は含まれません。したがって、軸を解答には含めず、軸以外の変域で考えます。 x=-2よりx=1の方が遠いので 最大値f(-2)=(-2) ²-4×(-2)+6 =14 最小値なし ← x<1より1は含めないため「0」ではなく「なし」となります。
次に、応用問題です
(2)f(x)=x²-2ax-a+6(0≦x≦4)について、
(ア)最大値を求めましょう。
(イ)最小値を求めましょう。
解き方
まず、軸を求めます。x=aとなります。
ここで大切な点として、最大値を考える場合、軸x=aと変域0≦x≦4の中央値2を比べることです。
(イ) の最小値の場合、軸に近いほど最小値になるため、変域0≦x≦4の内外に軸があるかを考える。
1. x = aが0≦x≦4より左側の外にある。つまり、a<0のときx=0の方がx=4より近いので、
f(0) = -a + 6
2. x = aが0≦x≦4の内にある。つまり、a≦a≦4のときx=aが最小値をとる。
f(a) = a²-2a²-a 6
=-a²-a+6
3. x = aが0≦x≦4より右側の外にある。つまり、4<aのときf(4)=-9a+22

ポイントとして、x=a が変域0≦x≦4の
左外→内で左より→中央→内で右より→右外
とaをずらしていくことで解けるのです。
最後に、以下の問題を考えてみましょう
(3) f(x)=x²-6+5(a≦x≦a+2)のとき、最大値・最小値を求めましょう。
解き方 まず、軸x=3を求めます。
次に、軸x=3と変域a≦x≦a+2の中央値
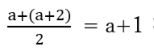
を比べます。
最大値は
1. a+1≦3のとき、つまりa≦2のとき、x=aの方が遠いので
f(a)=a²-6a+5
※a+1=2の場合を個別に解く必要はありません。
(ア) 最大値
aと中央値2の位置で場合分けします。
1. a≦2(中央値より左か中央値と同じ)
x=0よりx=4の方が遠いので
f(4)=4²-2a×4-a+6
=16-9a+6
=-9a+22
※a=2→中央値と同じでも特定の値になるだけで、最大値の位置は同じです。
x=0.4が最大値より、
f(0)=-a+6=-2+6=4
2.2<a(中央値より右)
x=4よりx=0の方が遠いので、f(0)=-a+6
以上より

3.3<a+1のとき、つまり2<aのときx=a+2の方が遠いので
f(a+2)=(a+2) ²-6(a+2)+5
=a²+4a+4-6a-12+5
=a²-2a-3

最小値は 変域a≦x≦a+2の内外に軸x=2があるかを比べます。
1. a+2≦3のとき、つまりa≦1のとき、x=a+2が近いので
f(a+2)=a²-2a-3
2. a<3≦a+2のとき、つまり、4≦a<3のとき、
f(3)=3²-6×3+5=-4
3. 3≦aのときf(a)=a²-6a+5
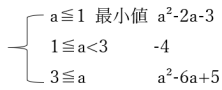
ポイント
下に凸グラフの場合分けは、基本的に
最大値は2つ
最小値は3つ の場合分けが出来ます。
まとめ
変域を固定し、左外から順に軸を動かしていくことで、最大値、最小値は解けるようになっています。
こちらの記事を読まれたお子さまへ
もしも勉強のことでお困りなら、親御さんに『アルファ』を紹介してみよう!

「勉強のやり方が分からない!」
「何から始めれば良いの??」
「前回のテストの点数、ちょっとやばかったな…」
そんなことでお困りではありませんか?
『家庭教師のアルファ』なら、あなたにピッタリの家庭教師がマンツーマンで勉強を教えてくれるので、
どんなに今の学力や成績に自信がなくても、着実に力を付けていくことがでいます!
もしも今、ちょっとでも家庭教師に興味があれば、ぜひ親御さんへ『家庭教師のアルファ』を紹介してみてください!
下のボタンから、アルファの紹介ページをLINEで共有できます!
こちらの記事をお読みいただいた保護者さまへ
さて、この記事をお読み頂いた方の中には
「子どもが高校生になってから苦手な科目が増え、成績も落ち始めた」
「部活が忙しくて勉強する時間がとれない」
「このままだと大学受験が心配」
といった、お子さまの勉強に関するお悩みを持たれている方も多いのではないでしょうか。
高校生は中学生に比べ学習量が圧倒的に多くなり、勉強の難度も上がるため、一気に挫折してしまうお子さまも多いのです。
高校生の効率的な成績向上・受験対策を行うには、現在の到達度を分析し、お子さまの状況にあわせた学習を行う必要があります。
ただ、お子さま一人で自身の現状を分析し、学習カリキュラムを組み上げるのは困難な場合がほとんどです。
家庭教師のアルファが提供する完全オーダーメイド授業は、一人ひとりのお子さまの状況を的確に把握し、学力のみならず、性格や生活環境に合わせた指導を行います。もちろん、受験対策も志望校に合わせた対策が可能ですので、合格の可能性も飛躍的にアップします。特に大学受験の場合、早い段階から学習カリキュラムを立て、計画的に対策を進める必要があるので、家庭教師は良きプランナーとしての役割も果たします。
高校生のお子さまの勉強についてお困りの方は、是非一度、プロ家庭教師専門のアルファの授業を体験してみてください。下のボタンから、無料体験のお申込みが可能です。
こちらの記事の監修者

浅井保(あさい たもつ)
- ・北海道大学文学部卒
- ・家庭教師のアルファ 講師部長
2008年に『家庭教師のアルファ』のプロ家庭教師として活動開始し、数多くの生徒への学習指導を経験。
現在、株式会社アルファコーポレーション講師部部長。











