目次
「円」とは
小学生のときにコンパスを使って円をかいたことは最低1度はあると思いますが、円は数学的に考えるとある点Oから等しい距離(=半径r)の集合でできる曲線のこと。
つまり円には中心と半径が必要なのです。
円の方程式って何?
↑で述べたことを踏まえ、ある点Oが円の中心の座標を(a,b)、半径をrとすると
(x-a)2+(y-b)2=r2…(i)
となります。中心を原点(0,0)とすると
x2+y2=r2
になります。これは直角三角形の三平方の定理から導かれています。
(底辺の二乗+高さの二乗=半径(=斜辺)の二乗)
また(i)の式を展開すると
x2+y2-2ax-2by+a2+b2-r2=0
となり、
x2+y2+Ax+By+C=0…(ii)
の形でA、B、Cの値を導ければこれも円の方程式となります。
円の方程式を求め方
①:中心と半径がわかっている円の方程式を求める
それでは②で求めた円の方程式の公式から問題を解いてみましょう。
「中心が原点で、半径3の円」は(i)の式でa=0、b=0、r=3を代入して
x2+y2=9
となります。「中心が(2,3)で、半径4の円」ならば同じく(i)の式にa=2、b=3、r=4を代入して
(x-2)2+(y-3)2=16
となります。代入するだけなのでとても簡単だと思います。
それではこれではどうでしょうか?
「中心(2,3)でx軸に接する円」を求めてください。一見半径がわからないと思うかもしれません。この場合は中心のy座標から半径がわかります。つまりr=3なのです。
よって(i)の式にa=2、b=3、r=3なので
(x-2)2+(y-3)2=9
となります。
「中心(2,3)でy軸に接する円」を求めてください。この場合は中心のx座標から半径がわかります。つまりr=2なのです。
よって(i)の式にa=2、b=3、r=2なので
(x-2)2+(y-3)2=4
もしわからない場合は図を書いて考えてみるようにしましょう。
円の方程式を求め方
②:中心とある点を通る円の方程式を求める
「中心が(4,5)で、点(3,2)を通る円」の方程式を求めてみましょう。
まず、(i)の式にa=4、b=5を代入して
(x-4)2+(y-5)2=r2
とここまで式を作れました。次に点(3,2)を通ることからx=3、y=2を代入して
(3-4)2+(2-5)2=r2
1+9=r2
r2=10
r>0より
r=√10
となり、半径を求めることができました。
したがって求める円の方程式は
(x-4)2+(y-5)2=10
となります。
円の方程式を求め方
③:2点を直径の両端とする円の方程式を求める
「2点A (2,1)、B(4,-3)を直径の両端とする円」の方程式を求めてみましょう。
まず中心を求めます。
中心Cは線分A Bの中点で、中心の座標は
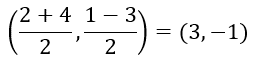
また半径は
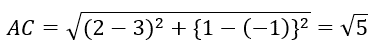
となるので円の方程式は
![]()
と求められます。
円の方程式を求め方
④:3点から円の方程式を求める
「3点A(-2,2)、B(1,3)、C(-1,-1)を通る円」の方程式を求めてみましょう。
これは(ii)の式を使います。
Aの座標を代入すると
-2A+2B+C+8=0…①
Bの座標を代入すると
A+3B+C+10=0…②
Cの座標を代入すると
-A-B+C+2=0…③
これら①、②、③の式からA=0、B=–2、C=–4となって3点を通る円の方程式は
x2+□2-2y-4=0
と求められます。
円の方程式を求め方
⑤:一般形の円の方程式から円の中心と半径を求める
一般形の円の方程式から基本形に直して円の中心と半径を求める問題です。
問:次の方程式は、どのような図形を表すか答えなさい
x2+y2-10x+6y+30=0
この問題のポイントはx2+y2の項があることに着目します。
必然的に円になるのですが、x2+y2の部分とxyがないことに注目しなければ
「円」になることに気がつきません。
それではどうするのか、2次関数で使った「平方完成」です。
x2+y2-10x+6y+30=0
平方完成すると
x2-10x+25+y2+6y+9-4=0
(x-5)2+(y+3)2=4
中心が(5,―3)、半径が2の円になるのです。
一般形から基本形に換算するようにもできるようになりましょう。
まとめ
円の方程式を求めるには2つの形を使い分けることがポイントです。
(x-a)2+(y-b)2=r2…(i)
x2+y2+Ax+By+C=0…(ii)
(i)は中心や半径がわかっているときに使う形です。(i)の形を基本形といいます。
(ii)は3点の座標がわかっているときのみ使います。(ii)の形を一般形といいます。
基本形の問題は種類が多いのでたくさんのパターンに取り組むのが良いです。
また一般系の問題は3元1次連立方程式の計算練習が必要になってきます。
符号や平方根などケアレスミスいやすいところでもあるので丁寧な計算をしてどんな問題でも正解できるようにしましょう!








