目次
微分とは?
微分とは、数学の分野である解析学において、関数の値が微小な変化をした場合の変化量と、その瞬間の傾きを表すものです。
つまり、微分は関数の変化の割合を表す操作であり、数学や物理学などの分野でも広く応用されています。
微分は、関数が滑らかな曲線で表される場合、曲線上の点での接線の傾きを求めることによって、その点における傾きや変化量を表現したりもできます。
微分を用いることで、関数の最大値や最小値、接線、接点などの関数についての様々な情報を得ることができます。
つまり、微分を使うことによって、その関数についてもっと色々深く知ることができる、ということですね。
微分の求め方と解釈方法
微分を求めるためには、以下の手順を行います。
微小量を決定する。
微小量で関数の変化量を求める。
微小量を0に近づけていく極限を求める。
具体的には、関数f(x)の微分を求める場合、以下の式で表されます。
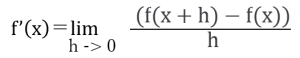
この式で、hは微小量を表し、f(x + h) – f(x)は関数f(x)の微小な変化量を表します。
式の分母であるhを0に近づけることで、f(x)の微小な変化量の極限を求めることができます。
ここで求められた新しい関数f'(x) を導関数と呼び、導関数を求めることを「微分する」と言います。
微分はある関数の変化の割合を表すため、関数がどのような傾向を持っているかを知ることができます。
例えば、微分が正であれば関数が増加していることを示し、微分が負であれば関数が減少していることを示します。
微分の基本公式
微分の基本公式は以下のようになります。
1:定数倍の微分公式
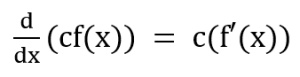
2:和の微分公式
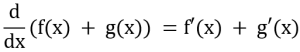
3:差の微分公式
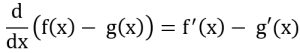
4:積の微分公式
![]()
5:商の微分公式
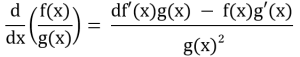
更に、一般にf(x)=xnの微分はf’(x)=nx{n-1}であることが知られています。
これらの公式を利用することで、複雑な関数の微分を簡単に求めることができます。
例えば、積の微分公式を用いると、2つの関数の積の微分は、各関数の微分と積をとったものを足し合わせたものになります。
同様に、商の微分公式を用いると、2つの関数の商の微分は、分子の微分と分母の微分を用いた式になります。
微分を用いた関数の解析
微分を用いることで、関数の極大値や極小値、接線、接点などの情報を得ることができます。
以下に、微分を用いた関数の解析方法について解説します。
関数の増減と凸凹
関数の増減とは、関数の値が増加するか、減少するかを表します。
関数の凸凹とは、関数のグラフが上に凸であるか、下に凸であるかを表します。
関数の増減や凸凹を求めるためには、以下の手順を行います。
1.関数の微分を求める。
2.微分が正であれば関数は増加し、負であれば関数は減少する。
(凹凸については、ちょっと高度になるので省略します)
関数の極大値・極小値
ある関数の極大値とは、その点の周辺において、その値よりも大きい値をとることができない値のことを言います。
同様に、関数の極小値とは、その点の周辺において、その点よりも小さい値をとることができない値のことを言います。
関数の極大値や極小値を求めるためには、以下の手順を行います。
1.関数の微分を求める。
2.微分が0になるような点を求める。
3.その点の前で微分が正、その点の後で微分が負の値をとる時は、極大値となる
4.その点の前で微分が負、その点の後で微分が正の値をとる時は、極小値となる
曲線の接線と接点
微分は、曲線の接線を求めるためにも使われます。
曲線上の点Pにおける接線は、その点での接線の傾きを微分を使って求めることにより得ることができます。
この接線の傾きは、曲線上の点Pにおける微分係数となります。
曲線上の点Pにおける接線の方程式は、次のように表されます。
y – f(x₀) = f'(x₀)(x – x₀)
ここで、(x₀, y₀)は曲線上の点Pの座標、f(x)は曲線上の関数、f'(x₀)はx = x₀におけるf(x)の微分係数です。
また、曲線上の点Pにおける接点は、曲線上の点Pと接線が交わる点です。
例えば、曲線y = x^2 – 3x + 2の点(1, 0)における接線と接点を求める場合、以下のように計算します。
まず、f(x) = x2 – 3x + 2として、f'(x)を求めます。
f'(x) = 2x – 3
次に、x = 1におけるf(x)とf'(x)を求めます。
f(1) = 12 – 3(1) + 2 = 0
f'(1) = 2(1) – 3 = -1
したがって、点(1, 0)における接線の方程式は、
y – 0 = -1(x – 1)
つまり、y = -x + 1となります。
微分の応用について
推定、近似、最適化問題
微分を用いる最も一般的な応用分野の1つは、関数の近似と最適化です。
例えば、ある関数が与えられたとき、その関数が最小または最大になる値を見つけることができます。
これは、最適化問題と呼ばれます。
また、ある関数が与えられた場合、その関数が与えられたデータに最もよくフィットするような近似関数を見つけることもできます。
これは、近似問題と呼ばれます。
例えば、実験結果から得られたデータをもとに、関数のグラフを近似することで、実験結果を予測することができます。
また、微分を用いて、ある関数が最適な設計や生産プロセスを導くことができます。
例えば、ある工場がある製品を製造するとき、製品の品質や生産効率を向上させるために、製品の設計や生産プロセスを最適化する必要があります。
微分を用いることで、関数を最適化することができます。
物理学、工学などへの応用
微分は、物理学、工学、経済学、統計学などの幅広い分野で応用されています。
物理学においては、微分を用いて物体の運動を解析したり、物体の速度や加速度を求めたりすることができます。
また、微分を用いて電気回路や制御システムなどの設計や解析にも応用されます。
工学においては、微分を用いて構造物の応力や変形を解析したり、材料の特性を評価したりすることができます。
また、微分を用いて、機械やエネルギーシステムなどの設計や制御にも応用されます。
まとめ
微分は、高校数学の中でも重要な概念の一つであり、数学の他の分野や物理学、工学などの科学技術分野においても広く用いられています。
微分を使うことで、関数の傾きや変化の速さ、最大値や最小値、接線や接点などを求めることができます。
また、微分を応用することで、推定、近似、最適化問題の解決や物理学、工学などへの応用も可能です。
微分の理解は、数学だけでなく、様々な分野での問題解決においても重要な役割を果たします。
みなさんも、単に計算方法を学ぶだけでなく、このような応用についても知っていくと、より微分に対する興味が湧いてくるかもしれませんね。頑張ってください!








