目次
標準偏差とは

標準偏差とはデータの散らばり具合を表す値で次のように定義されます。
■定義
データX1,X2,,X3,・・・X,n,に対してその平均値をX ̅とすると、標準偏差sは
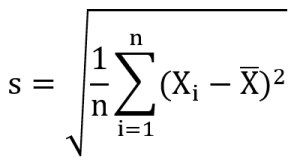
となりますが、これを見て「ああなるほどな」と思う人はあまり居ないでしょう。
重要なのは、この標準偏差というものが「どのようにして考えられたのか」という過程の方です。
データの散らばり
冒頭でデータの散らばり具合を表す値といいましたが、中学校で同じくデータの散らばりを表す値として範囲、及び四分位範囲がありました。
しかし、範囲ではデータを2つしか使っていないうえ、外れ値と呼ばれる1つだけ他のデータに比べて大きすぎる、または小さすぎる値の影響を受けやすいということが問題点としてあります。
その問題点は、四分位範囲においては解消されたものの、やはり使われていないデータがあるという問題点が残ります。
なんとかすべてのデータを使ってデータの散らばりを表す方法はないか・・・と、そこで考えられたのが標準偏差です。
標準偏差の意味
ではどのようにしてすべてのデータを使ってデータの散らばりを表せばいいのか。
それは「平均からの離れ具合の平均」です。
例えば平均点50点のテストがあったとします。
この時の標準偏差が1点であれば49点~51点くらいの人が多く、標準偏差が2点であれば48点~52点くらいの人が多いということになります。
つまり、後者の方が「散らばっている」と評価できるわけですね。
これなら全てのデータを使いデータの散らばり具合を表せそうです。
標準偏差の導出
平均からの離れ具合は平均との差のことなので(Xi–X)と表せます。
これを偏差といいます。
ですがこれらの平均値、すなわち
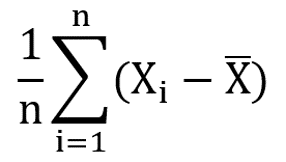
となりますが、これは計算すると必ず0になってしまいます。
これは(Xi–X)
が負になる場合もあるためです。
なので全て正にするために2乗の平均をとります。
すなわち
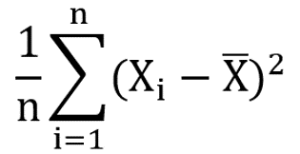
です。これを分散といってs2と表します。
これは実際のデータを2乗した値の平均のためこの分散の値の正の平方根をとった値
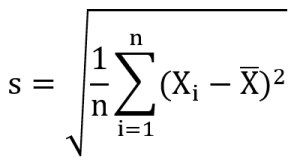
これを標準偏差と定義します。
このようにただ漠然と公式を暗記するよりも、過程の部分を見ることで標準偏差の意味を理解しやすいと思います。
標準偏差に限らず、高校数学では公式や定理が数多く出てきますが、結果だけでなく過程の部分をしっかり理解することが大切です。
おまけ
受験生は嫌でも意識しなければならない数字に偏差値というものがありますが、これは標準偏差をもとに算出されています。
算出する式は次のとおりです。
偏差値=50+10×(自分の得点-平均点)÷標準偏差
要は、50を基準に平均点から標準偏差の1/10の点ごとに1ずつ増減します。
偏差値60以上は全体の約16%、70以上は約2%ほどと言われています。
偏差値は自分の位置を知る数値ですが、周りの影響を大きく受ける値です。
これは筆者の今までの経験ですが、公開されている偏差値に達していなくても合格できたり、その逆も見てきました。
そのため偏差値という数字に縛られすぎず、あくまで「大まかな参考値」程度の認識で大丈夫です。








